(本小题满分14分)已知数列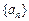 的前
的前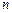 项和
项和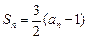 ,
,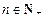 .
.
(1)求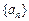 的通项公式;(2)设
的通项公式;(2)设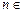 N+,集合
N+,集合 ,
,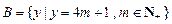 .现在集合
.现在集合 中随机取一个元素
中随机取一个元素 ,记
,记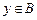 的概率为
的概率为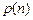 ,求
,求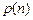 的表达式.
的表达式.
若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:mm),将所得数据分组,得到如下频率分布表:
| 分 组 |
频 数 |
频 率 |
| [-3,-2) |
0.10 |
|
| [-2,-1) |
8 |
|
| (1,2] |
0.50 |
|
| (2,3] |
10 |
|
| (3,4] |
||
| 合计 |
50 |
1.00 |
(1)将上面表格中缺少的数据填充完整.
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率.
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品.据此估算这批产品中的合格品的件数.
某单位最近组织了一次健身活动,参加活动的职工分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
(1)游泳组中青年人、中年人、老年人分别所占的比例.
(2)游泳组中青年人、中年人、老年人分别应抽取的人数.
某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3000名初中生、4000名高中生中作问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
(3)为了从4000份高中生的答卷中抽取一个容量为64的样本,如何使用系统抽样抽取到所需的样本?
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xn,…,x2008;y1,y2,…,yn,…,y2008.
(1)求数列{xn}的通项公式.
(2)写出y1,y2,y3,y4,由此猜想出数列{yn}的一个通项公式yn,并证明你的结论.
(3)求zn=x1y1+x2y2+…+xnyn(n∈N*,n≤2008).
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xk,…;y1,y2,…,yk,….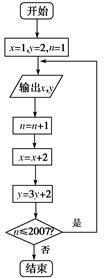
(1)分别求数列{xk}和{yk}的通项公式;
(2)令zk=xkyk,求数列{zk}的前k项和Tk,其中k∈N*,k≤2 007.