若存在实数k，b，使得函数
和
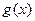对其定义域上的任意实数x同时满足：
，则称直线：
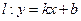为函数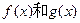
的“隔离直线”。已知
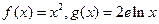（其中e为自然对数的底数）。试问：
（1）函数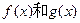的图象是否存在公共点，若存在，求出交点坐标，若不存在，说明理由；
（2）函数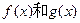是否存在“隔离直线”？若存在，求出此“隔离直线”的方程；若不存在，请说明理由。
在
中，已知
，
.
(Ⅰ)求
的值；
(Ⅱ)若
为
的中点，求
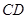的长.
为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计 |
５０ |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
．
（1）请将上面的列联表补充完整；
（2）是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关？说明你的理由.下面的临界值表供参考：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005] |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式：
，其中
)
已知连续型随机变量
的概率密度函数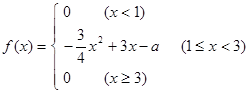
，
（1）求常数
的值，并画出的概率密度曲线；
（2）求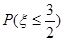 
．
甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为
；乙用这枚硬币掷2次，记正面朝上的次数为
。
（1）分别求与的期望；
（2）规定：若
，则甲获胜；若
，则乙获胜，分别求出甲和乙获胜的概率.
为了考察某种中药预防流感效果，抽样调查40人，得到如下数据：服用中药的有20人，其中患流感的有2人，而未服用中药的20人中，患流感的有8人。
（1）根据以上数据建立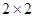
列联表；
（2）能否在犯错误不超过0.05的前提下认为该药物有效？
参考
 |
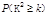0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
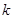0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
（
）
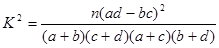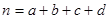