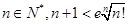已知函数 的图象可由函数
的图象可由函数 的图象向左平移
的图象向左平移 个单位得到。
个单位得到。
(1)求函数 的的解析式和最小正周期;
的的解析式和最小正周期;
(2)在中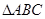 ,内角A、B、C所对的边分别为a、b、c,若
,内角A、B、C所对的边分别为a、b、c,若 ,求
,求 得值;
得值;
设函数 .
.
(1)求不等式 的解集;
的解集;
(2)若存在x使不等式 成立,求实数a的取值范围.
成立,求实数a的取值范围.
在直角坐标系xOy中,已知点P ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
.
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与直线C的两个交点为A、B,求 的值.
的值.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.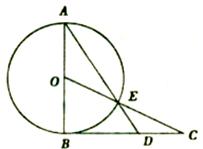
(1)求证:CE2 =" CD" · CB;
(2)若AB =" BC" = 2,求CE和CD的长.
已知函数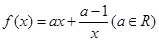 ,
,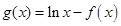 .
.
(1)若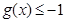 对于任意的
对于任意的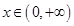 恒成立,求实数
恒成立,求实数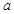 的取值范围;
的取值范围;
(2)求证:对任意