在直角坐标系xOy中,已知点P ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
.
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与直线C的两个交点为A、B,求 的值.
的值.
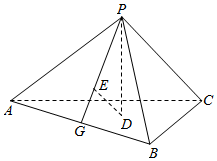
如图,已知正三棱锥 的侧面是直角三角形, ,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
设
,向量
,
,
,
.
(1)若
,求
;
(2)若
,求
的值;
(3)若
,求证:
.
已知
,
.
(1)求
的值;
(2)求
的值.
已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.
如图,在△OAB中,已知P为线段AB上的一点,且|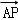 |=2|
|=2| |.
|.
(Ⅰ)试用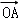 ,
, 表示
表示 ;
;
(Ⅱ)若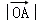 =3,
=3,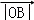 =2,且∠AOB=60°,求
=2,且∠AOB=60°,求 •
•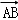 的值.
的值.