(本小题满分14分)如果对于函数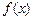 的定义域内任意的
的定义域内任意的 ,都有
,都有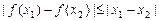 成立,那么就称函数
成立,那么就称函数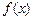 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数 ,
,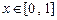 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数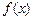 是闭区间
是闭区间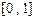 上的“平缓函数”,且
上的“平缓函数”,且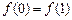 .证明:对于任意的
.证明:对于任意的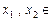
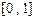 ,都有
,都有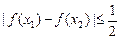 成立.(3)设
成立.(3)设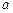 、
、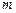 为实常数,
为实常数,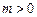 .若
.若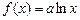 是区间
是区间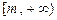 上的“平缓函数”,试估计
上的“平缓函数”,试估计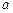 的取值范围(用
的取值范围(用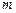 表示,不必证明).
表示,不必证明).
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设
为取出的4个球中红球的个数,求
的分布列和数学期望.
已知函数
.
(Ⅰ)求函数
的最小正周期;
(Ⅱ)求函数
在区间
上的最小值和最大值.
已知函数
在区间
,
内各有一个极值点.
(I)求
的最大值;
(II)当
时,设函数
在点
处的切线为
,若
在点
处穿过函数
的图象(即动点在点
附近沿曲线
运动,经过点
时,从
的一侧进入另一侧),求函数
的表达式.
设
是数列
(
)的前
项和,
,且
,
,
.
(I)证明:数列
是常数数列;
(II)试找出一个奇数
,使以18为首项,7为公比的等比数列
中的所有项都是数列
中的项,并指出
是数列
中的第几项.
已知双曲线
的右焦点为
,过点
的动直线与双曲线相交于
两点,点
的坐标是
.
(I)证明
,
为常数;
(II)若动点
满足
(其中
为坐标原点),求点
的轨迹方程.