已知椭圆的中心在原点,焦点为F1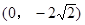 ,F2(0,
,F2(0, ),且离心率
),且离心率 。
。
(I)求椭圆的方程;
(II)直线l(与坐标轴不平行)与椭圆交于不同的两点A、B,且线段AB中点的横坐标
为 ,求直线l的斜率的取值范围。
,求直线l的斜率的取值范围。
已知函数 .
.
(1)当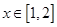 时,
时,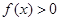 恒成立,求实数
恒成立,求实数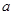 的取值范围;
的取值范围;
(2)若函数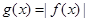 (
(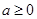 )在
)在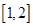 上是增函数,求实数
上是增函数,求实数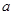 的取值范围.
的取值范围.
已知二次函数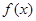 满足
满足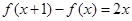 (
( ),且
),且 .
.
(1)求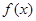 的解析式;
的解析式;
(2)若函数 在区间
在区间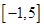 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(3)若关于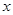 的方程
的方程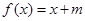 有区间
有区间 上有唯一实数根,求实数
上有唯一实数根,求实数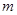 的取值范围(注:相等的实数根算一个).
的取值范围(注:相等的实数根算一个).
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益函数是 其中
其中 是仪器的产量(单位:台):
是仪器的产量(单位:台):
(1)将利润 表示为产量
表示为产量 的函数(利润
的函数(利润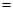 总收益
总收益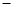 总成本);
总成本);
(2)当产量 为多少台时,公司所获利润最大?最大利润是多少元?
为多少台时,公司所获利润最大?最大利润是多少元?
已知 .
.
(1)判断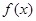 奇偶性并证明;
奇偶性并证明;
(2)判断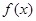 单调性并用单调性定义证明;
单调性并用单调性定义证明;
(3)若 ,求实数
,求实数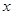 的取值范围.
的取值范围.
(1)已知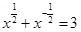 ,求
,求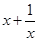 的值;
的值;
(2)计算: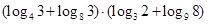 .
.