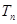已知非零向量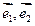 不共线,且
不共线,且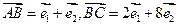 ,
,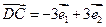 ,
,
(1)求证:A、B、D三点共线
(2)试确定实数k的值,使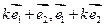 共线
共线
(本小题满分13分)
如图,在正四面体 中,
中, 分别是棱
分别是棱 的中点.
的中点.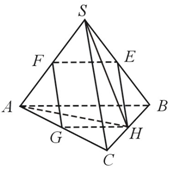
(1)求证:四边形 是平行四边形;
是平行四边形;
(2)求证: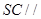 平面
平面 ;
;
(3)求证: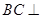 平面
平面 .
.
(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是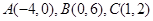 .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线 平行的直线方程;
平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为 ,求
,求 与两坐标轴围成的三角形的面积.
与两坐标轴围成的三角形的面积.
设函数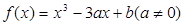
(1)若曲线 在点
在点 处的切线方程是
处的切线方程是 ,求
,求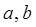 的值
的值
(2)求函数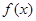 的单调区间及极值
的单调区间及极值
已知椭圆C: 的左焦点
的左焦点 坐标为
坐标为 ,且椭圆C的短轴长为4,斜率为1的直线
,且椭圆C的短轴长为4,斜率为1的直线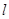 与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为
与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为 .
.
(1)求椭圆C的方程
(2)求 的面积
的面积
已知等比数列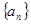 满足,
满足,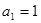 ,
,
(1)求数列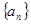 的通项公式
的通项公式
(2)若等差数列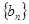 的前n项和为
的前n项和为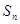 ,满足
,满足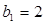 ,
,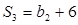 ,求数列
,求数列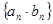 的前n项和
的前n项和