(本小题满分12分)如图,抛物线的顶点O在坐标原点,焦点在y轴的负半轴上,过点M(0,-2)作直线l与抛物线相交于A,B两点,且满足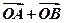 =(-4,-12).
=(-4,-12).
(1)求直 线l和抛物线的方程;
线l和抛物线的方程;
(2)当抛物线上一动点P在点A和B之间运动时,求ΔABP面积的最大 值.
值.
如图,直三棱柱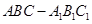 的底面
的底面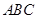 是等腰直角三角形,
是等腰直角三角形,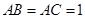 ,侧棱
,侧棱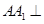 底面
底面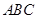 ,且
,且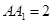 ,
,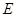 是
是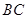 的中点,
的中点,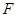 是
是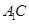 上的点.
上的点.
(1)求异面直线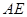 与
与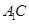 所成角
所成角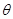 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
(2)若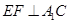 ,求线段
,求线段 的长.
的长.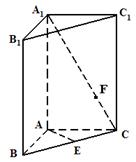
已知函数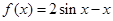 ,
,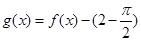 .
.
(1)讨论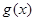 在
在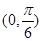 内和在
内和在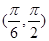 内的零点情况.
内的零点情况.
(2)设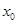 是
是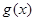 在
在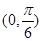 内的一个零点,求
内的一个零点,求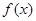 在
在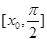 上的最值.
上的最值.
(3)证明对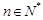 恒有
恒有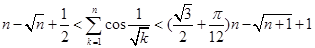 .[来
.[来
椭圆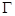 :
: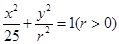 的左顶点为
的左顶点为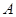 ,直线
,直线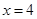 交椭圆
交椭圆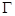 于
于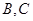 两点(
两点(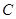 上
上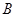 下),动点
下),动点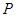 和定点
和定点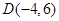 都在椭圆
都在椭圆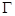 上.
上.
(1)求椭圆方程及四边形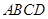 的面积.
的面积.
(2)若四边形 为梯形,求点
为梯形,求点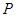 的坐标.
的坐标.
(3)若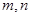 为实数,
为实数,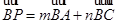 ,求
,求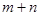 的最大值.
的最大值.
如图,已知平面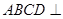 平面
平面 ,且四边形
,且四边形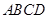 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, ,
,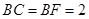 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设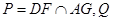 是直线
是直线 上的动点,判断并证明直线
上的动点,判断并证明直线 与直线
与直线 的位置关系.
的位置关系.
(3) 求三棱锥 的体积.[来.
的体积.[来.
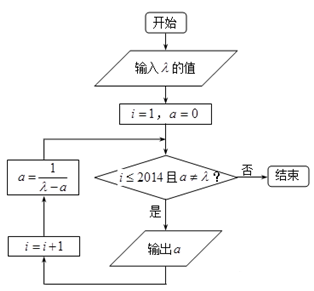
执行如图所描述的算法程序,记输出的一列 的值依次为
的值依次为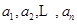 ,其中
,其中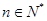 且
且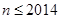 .
.
(1)若输入 ,写出全部输出结果.
,写出全部输出结果.
(2)若输入 ,记
,记 ,求
,求 与
与 的关系(
的关系(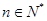 ).
).