假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
| x |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
设AB=6,在线段AB上任取两点(端点A、B除外),将线段AB分成了三条线段,
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形的概率.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组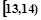 ;第二组
;第二组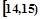 ……第五组
……第五组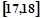 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设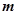 、
、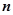 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知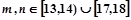 .
.
求事件“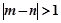 ”的概率.
”的概率.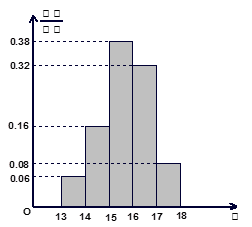
已知函数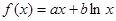 .
.
(I)当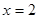 时
时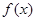 取得极小值
取得极小值 ,求
,求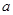 、
、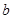 的值;
的值;
(II)当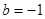 时,若在区间
时,若在区间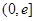 上至少存在一点
上至少存在一点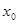 ,使得
,使得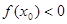 成立,求实数
成立,求实数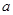 的取值范围.
的取值范围.
已知抛物线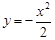 与过点
与过点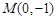 的直线
的直线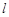 相交于
相交于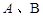 两点,
两点,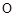 为原点.若
为原点.若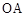 和
和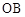 的斜率之和为1,(1)求直线
的斜率之和为1,(1)求直线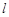 的方程; (2)求
的方程; (2)求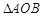 的面积.
的面积.
某商场销售某种商品的经验表明,该商品每日的销售量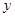 (单位:千克)与销售价格
(单位:千克)与销售价格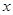 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式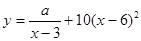 ,其中
,其中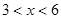 ,
,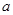 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求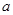 的值;
的值;
(2) 若该商品的成本为3元/千克, 试确定销售价格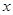 的值,使商场每日销售该商品所获得的利润最大.(利润=销售额-成本)
的值,使商场每日销售该商品所获得的利润最大.(利润=销售额-成本)