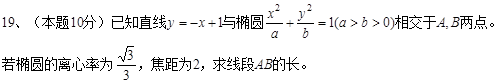、某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是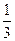 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
(3)求这名学生在上学路上因遇到红灯停留的总时间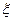 的分布列、期望及方差
的分布列、期望及方差
(本小题10分)已知圆 经过
经过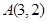 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.
(1) 求圆 的方程;
的方程;
(2) 若直线 经过点
经过点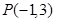 且与圆
且与圆 相切,求直线
相切,求直线 的方程.
的方程.
(本小题10分)如图已知在三棱柱ABC——A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
(1) 求证:面PCC1⊥面MNQ;
(2) 求证:PC1∥面MNQ。
(本小题8分)已知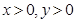 且
且 ,求
,求 的最小值
的最小值
(本题10分)如图一边长为48cm的正方形铁皮,四角各截去一个大小相同的小正方形,然后折起,可以做成一个无盖长方体容器。所得容器的体积V(单位: )是关于截去的小正方形的边长x(单位:
)是关于截去的小正方形的边长x(单位: )的函数。⑴ 随着x的变化,容积V是如何变化的?
)的函数。⑴ 随着x的变化,容积V是如何变化的?
⑵ 截去的小正方形的边长为多少时,容器的容积最大?最大容积是多少?