已知函数 。
。
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若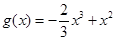 ,证明当
,证明当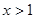 时,函数
时,函数 的图象恒在函数
的图象恒在函数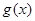 图象的上方.
图象的上方.
(本小题满分10分)
已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R
(1)求A∪B,(  A)∩B;
A)∩B;
(2)若A∩C≠ ,求a的取值范围。
,求a的取值范围。
(本小题满分12分)
已知椭圆C: (a>b>0)的右焦点为F
(a>b>0)的右焦点为F (1,0),离心率为
(1,0),离心率为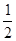 ,P为左顶点。
,P为左顶点。
(1)求椭圆C的方程;
(2)设过点F 的直线交椭圆C于A,B两点,若△PAB的面积为
的直线交椭圆C于A,B两点,若△PAB的面积为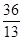 ,求直线AB的方程。
,求直线AB的方程。
(本小题满分12分)
设函数 ,曲线
,曲线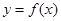 在点
在点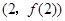 处的切线方程
处的切线方程 .
.
(1)求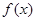 的解析式,并判断函数
的解析式,并判断函数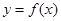 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
(2)证明:曲线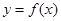 上任一点的切线与直线
上任一点的切线与直线 和直线
和直线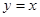 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
(3) 将函数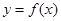 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线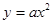 (
(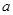 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)
(本小题满分12分)
已知数列 中,
中,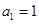 ,
, ,且
,且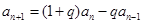
 .
.
(1)设 ,求
,求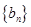 是的通项公式;
是的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)若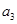 是
是 与
与 的等差中项,求
的等差中项,求 的值,并证明:对任意的
的值,并证明:对任意的 ,
,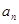 是
是 与
与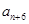 的等差中项.
的等差中项.
(本小题满分12分)
已知抛物线 :
: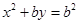 经过椭圆
经过椭圆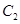 :
: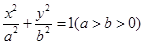 的两个焦点.设
的两个焦点.设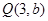 ,又
,又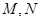 为
为 与
与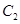 不在
不在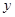 轴上的两个交点,若
轴上的两个交点,若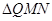 的重心(中线的交点)在抛物线
的重心(中线的交点)在抛物线 上,
上,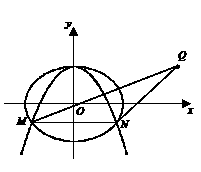
(1)求 和
和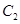 的方程.
的方程.
(2)有哪几条直线与 和
和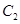 都相切?(求出公切线方程)
都相切?(求出公切线方程)