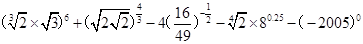已知数列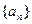 满足:
满足: ,且
,且
 (
( ).
). 
(1)求证:数列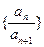 为等差数列;
为等差数列;
(2)求数列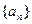 的通项公式;
的通项公式;
(3)求右表中前 行所有数的和
行所有数的和 .
.
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
已知函数 ,(x∈(- 1,1).
,(x∈(- 1,1).
(Ⅰ)判断f(x)的奇偶性,并证明;
(Ⅱ)判断f(x)在(- 1,1)上的单调性,并证明.
已知二次函数f(x)图象过点(0,3),它的图象的对称轴为x = 2,
且f(x)的两个零点的平方和为10,求f(x)的解析式.
定义在实数R上的函数y= f(x)是偶函数,当x≥0时,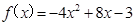 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明)
计算下列各式
(Ⅰ)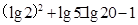
(Ⅱ)