商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
已知复数z=(2+i)m2--2(1-i).当实数m取什么值时,复数z是:
(1)虚数;(2)纯虚数;(3)复平面内第二、四象限角平分线上的点对应的复数?
已知函数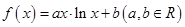 ,在点
,在点 处的切线方程是
处的切线方程是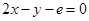 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数 的值及
的值及 的解析式;
的解析式;
(2)若 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式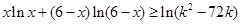 对一切
对一切 恒成立,求实数
恒成立,求实数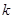 的取值范围。
的取值范围。
若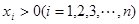 ,观察下列不等式:
,观察下列不等式: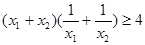 ,
, ,…,请你猜测
,…,请你猜测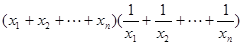 将满足的不等式,并用数学归纳法加以证明。
将满足的不等式,并用数学归纳法加以证明。
如图,点 为斜三棱柱
为斜三棱柱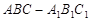 的侧棱
的侧棱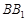 上一点,
上一点,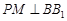 交
交 于点
于点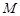 ,
,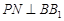 交
交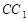 于点
于点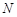 .
.
(1) 求证: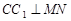 ;
;
(2) 在任意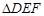 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
已知二次函数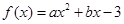 在
在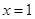 处取得极值,且在
处取得极值,且在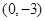 点处的切线与直线
点处的切线与直线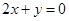 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数 在
在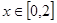 的最值。
的最值。