一个袋中装有四个形状大小完全相同的球,球的编号分别为
,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于
的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,求
的概率。
(满分10分)
已知集合 ,
,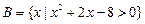 ,求
,求 .
.
已知 为坐标原点,
为坐标原点, 为椭圆
为椭圆 在
在 轴正半轴上的焦点,过
轴正半轴上的焦点,过 且斜率为
且斜率为 的直线
的直线 与
与 交与
交与 、
、 两点,点
两点,点 满足
满足

(Ⅰ)证明:点
 在
在 上;
上;
(Ⅱ)设点
 关于点
关于点 的对称点为
的对称点为 ,证明:
,证明: 、
、 、
、 、
、 四点在同一圆上。
四点在同一圆上。
已知函数

(Ⅰ)证明:曲线
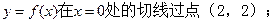
(Ⅱ)若
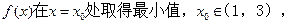 求
求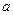 的取值范围。
的取值范围。
如图,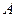 是以
是以 为直径的
为直径的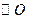 上一点,
上一点,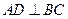 于点
于点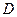 ,过点
,过点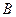 作
作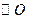 的切线,与
的切线,与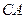 的延长线相交于点
的延长线相交于点 是
是 的中点,连结
的中点,连结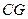 并延长与
并延长与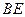 相交于点
相交于点 ,延长
,延长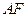 与
与 的延长线相交于点
的延长线相交于点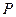 .
.
(1)求证: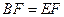 ;
;
(2)求证: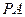 是
是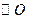 的切线;
的切线;
(3)若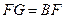 ,且
,且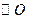 的半径长为
的半径长为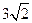 ,求
,求 和
和 的长度.
的长度.
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.