（本小题满分12分）
已知点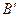
为圆
：
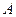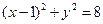上任意一点，点
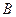(-1,0)，线段
的垂直平分线和线段
相交于点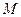
.
（Ⅰ）求点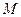的轨迹
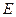的方程；
（Ⅱ）已知点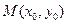
为曲线E上任意一点，
求证：点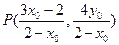
关于直线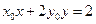
的对称点为定点，并求出该定点的坐标.
（本小题满分12分）已知命题
： 
表示焦点在
轴上的椭圆，命题
：
表示双曲线．若和有且仅有一个正确，求
的取值范围．
（本小题满分10分） 已知双曲线
的一条渐近线方程是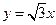
,它的一个焦点在抛物线
的准线上，（1）求双曲线的焦点坐标；（2）求双曲线的标准方程.
已知函数f（x）=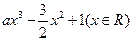
，其中a>0.
（1）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）若在区间
上，f（x）>0恒成立，求a的取值范围.
已知椭圆C的左、右焦点坐标分别是
，
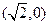，离心率是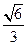
，直线y=t椭圆C交与不同的两点M，N，以线段MN为直径作圆P,圆心为P.
（1）求椭圆C的方程；
（2）若圆P与x轴相切，求圆心P的坐标；
已知函数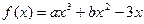
在
处取得极值。
（1）讨论
和
是函数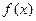
的极大值还是极小值；
（2）过点
作曲线
的切线，求此切线方程。