已知函数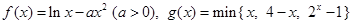 ,
, 是取
是取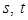 中较小者.
中较小者.
(1)求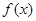 的单调区间和极值;
的单调区间和极值;
(2)若对于任意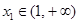 ,都存在
,都存在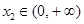 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x)图象的一条对称轴是直线 .
.
(I)求φ,并指出y=f(x)由y=sin2x作怎样变换所得.
(II)求函数y=f(x)的单调增区间;
(III)画出函数y=f(x)在区间[0,π]上的图象.
(1)已知tanα=2,求 + sin2α﹣3sinα•cosα的值。
+ sin2α﹣3sinα•cosα的值。
(2)已知角α终边上一点P(﹣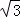 ,1),求
,1),求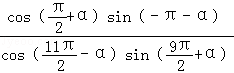 的值
的值
已知关于x的方程 的两根为sinθ和cosθ:
的两根为sinθ和cosθ:
(1)求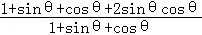 的值;
的值;
(2)求m的值.
(1)化简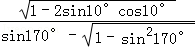 ;
;
(2)求值sin2120°+cos180°+tan45°﹣cos2(﹣330°)+sin(﹣210°)
已知数列{ }满足
}满足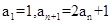 。
。
(1)求证:数列{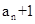 }是等比数列。
}是等比数列。
(2)求 的表达式。
的表达式。