(本小题满分12分)
已知椭圆C: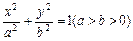 的长轴长为4.
的长轴长为4.
(1)若以原点为圆心,椭圆短半轴长为半径的圆与直线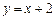 相切,求椭圆焦点坐标;
相切,求椭圆焦点坐标;
(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆交于M,N两点,直线PM,PN的斜率乘积为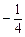 ,求椭圆的方程.
,求椭圆的方程.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
在数列{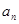 }中,
}中,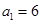 ,且
,且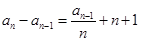
 ,
,
(1)求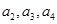 的值;
的值;
(2)猜测数列{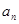 }的通项公式,并用数学归纳法证明。
}的通项公式,并用数学归纳法证明。
已知 .
.
若曲线 在
在 处的切线与直线
处的切线与直线 平行,求a的值;
平行,求a的值;
当 时,求
时,求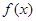 的单调区间.
的单调区间.
设不等式组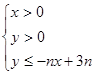 所表示的平面区域为
所表示的平面区域为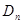 ,记
,记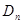 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为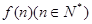
(1)求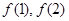 的值及
的值及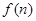 的表达式;
的表达式;
(2)设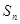 为数列
为数列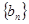 的前
的前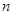 项的和,其中
项的和,其中 ,问是否存在正整数
,问是否存在正整数 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数 ;若不存在,说明理由
;若不存在,说明理由
在等差数列 中,
中, ,
,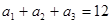 。
。
(1) 求数列 的通项公式;(2) 令
的通项公式;(2) 令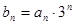 ,求数列
,求数列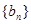 的前
的前 项和
项和