定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)> 0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
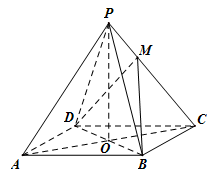
(本小题满分12分)如图,已知四棱锥 的底面是菱形,对角线
的底面是菱形,对角线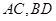 交于点
交于点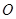 ,
,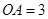 ,
,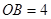 ,
,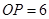 ,
,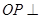 底面
底面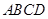 ,点满足
,点满足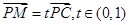 .
.
(1)当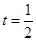 时,证明:
时,证明: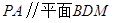 .
.
(2)若二面角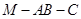 的大小为
的大小为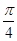 ,问:符合条件的点
,问:符合条件的点 是否存在.若存在,求出
是否存在.若存在,求出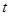 的值.若不存在,说明理由.
的值.若不存在,说明理由.
设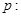 函数
函数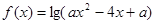 的值域为R;
的值域为R; 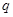 :不等式
:不等式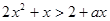 ,对
,对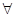
 ∈(-∞,-1)上恒成立,如果命题“
∈(-∞,-1)上恒成立,如果命题“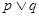 ”为真命题,命题“
”为真命题,命题“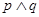 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知关于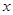 的二次函数
的二次函数
(Ⅰ)设集合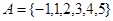 和
和 ,分别从集合
,分别从集合 ,
,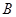 中随机取一个数作为
中随机取一个数作为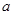 和
和 ,求函数
,求函数 在区间
在区间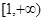 上是增函数的概率.
上是增函数的概率.
(Ⅱ)设点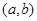 是区域
是区域 内的随机点,求函数
内的随机点,求函数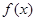 在区间
在区间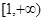 上是增函数的概率.
上是增函数的概率.
(本小题满分12分)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,200),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图.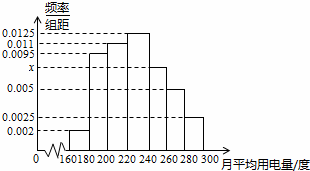
(1)求月平均用电量的众数和中位数;
(2)在月平均用电量为[220.240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[240.260)的用户中应抽取多少户?
(本小题满分10分)已知直线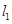 :
: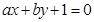 ,(
,(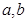 不同时为0),
不同时为0),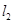 :
: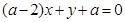 ,
,
(1)若 且
且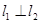 ,求实数
,求实数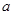 的值;
的值;
(2)当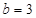 且
且 时,求直线
时,求直线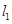 与
与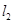 之间的距离
之间的距离