(本小题满分10分)已知直线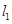 :
: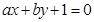 ,(
,(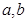 不同时为0),
不同时为0),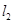 :
: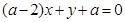 ,
,
(1)若 且
且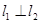 ,求实数
,求实数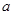 的值;
的值;
(2)当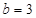 且
且 时,求直线
时,求直线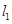 与
与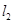 之间的距离
之间的距离
已知圆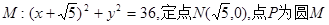 上的动点,点
上的动点,点 在
在 上,且满足|
上,且满足| |=|
|=| |
|
(1)求点 的轨迹
的轨迹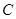 的方程;
的方程;
(2)过点(2,0)作直线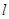 ,与曲线
,与曲线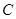 交于
交于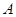 、
、 两点,
两点,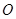 是坐标原点,设
是坐标原点,设 是否存在这样的直线
是否存在这样的直线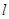 ,使四边形
,使四边形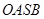 的对角线相等(即|
的对角线相等(即| |=|
|=| |)?若存在,求出直线
|)?若存在,求出直线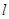 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
设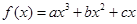 的极小值为
的极小值为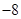 ,其导函数
,其导函数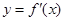 的图像开口向下且经过点
的图像开口向下且经过点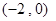 ,
,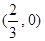 .
.
(1)求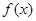 的解析式;
的解析式;
(2)若对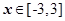 都有
都有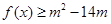 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
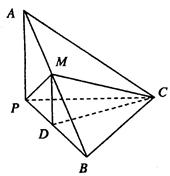
如图,已知三棱锥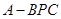 中,
中,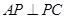 ,
, 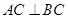 ,
,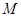 为
为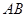 中点,
中点,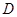 为
为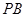 中点,且△
中点,且△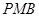 为正三角形。
为正三角形。
(1)求证: ∥平面
∥平面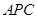 ;
;
(2)求证:平面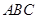 ⊥平面
⊥平面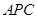 .
.
在各项均为正数的数列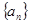 中,已知点
中,已知点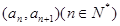 在函数
在函数 的图像上,且
的图像上,且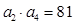 .
.
(1)求数列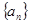 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列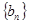 的前
的前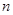 项和
项和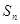 .
.
已知圆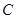 的方程为:
的方程为: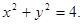 直线
直线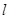 过点
过点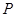 (1,2),且与圆
(1,2),且与圆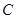 交于
交于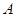 、
、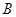 两点,若
两点,若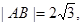 求直线
求直线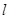 的方程;
的方程;