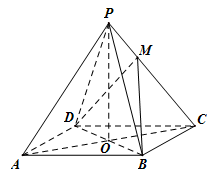
(本小题满分12分)如图,已知四棱锥 的底面是菱形,对角线
的底面是菱形,对角线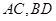 交于点
交于点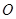 ,
,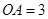 ,
,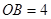 ,
,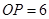 ,
,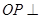 底面
底面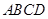 ,点满足
,点满足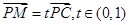 .
.
(1)当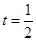 时,证明:
时,证明: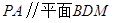 .
.
(2)若二面角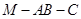 的大小为
的大小为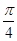 ,问:符合条件的点
,问:符合条件的点 是否存在.若存在,求出
是否存在.若存在,求出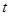 的值.若不存在,说明理由.
的值.若不存在,说明理由.
在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列(n∈N*).求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论.
某重点高校数学教育专业的三位毕业生甲、乙、丙参加了一所中学的招聘面试,面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是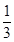 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:
(1)至少有1人面试合格的概率;(2)签约人数X的分布列.
(本题满分10 分)已知函数f(x)=x3-ax2+3x.
(1) 若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值和最小值.
(2) 若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;
设复数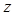 满足
满足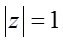 ,且
,且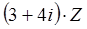 是纯虚数,求
是纯虚数,求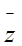 .
.
已知函数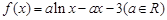 .
.
(I)当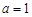 时,求函数
时,求函数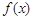 的单调区间;
的单调区间;
(II)若函数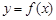 的图象在点
的图象在点 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的 ,函数
,函数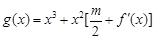 在区间
在区间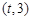 上总存在极值?
上总存在极值?