已知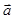 、
、 、
、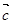 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中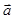
 .
.
(1)若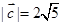 ,且
,且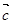 //
//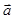 ,求
,求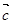 的坐标;
的坐标;
(2) 若|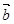 |=
|=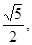 且
且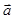 +2
+2 与
与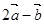 垂直,求
垂直,求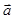 与
与 的夹角
的夹角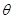 .
.
命题P:函数y=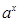 是增函数,命题q:对任意x都有
是增函数,命题q:对任意x都有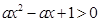 恒成立若“p或q”为真,“p且q”为假,求a的取值范围
恒成立若“p或q”为真,“p且q”为假,求a的取值范围
某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
(Ⅰ)求单位成本y与月产量x之间的线性回归方程.(其中已计算得: ,结果保留两位小数)
,结果保留两位小数)
(Ⅱ)当月产量为12千件时,单位成本是多少?
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:Cm),将周长整理后画出的频率分布表和频率分布直方图如下:观察图形,回答下列问题:
| 组距 |
频数 |
频率 |
|
 [ [ |
6 |
0.1 |
|
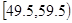 |
0.15 |
||
 |
9 |
||
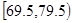 |
18 |
||
 |
0.25 |
||
 |
3 |
0.05 |
|
| 合计 |

(1)补充上面的频率分布表和频率分布直方图.
(2)79.5~89.5这一组的频数、频率分别是多少?
(3)估计这次环保知识竞赛的及格率(60cm及以上为合格
已知函数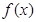 是定义在区间[-1.1]上的奇函数,且
是定义在区间[-1.1]上的奇函数,且 ,对于任意的m,n
,对于任意的m,n [-1,1]有
[-1,1]有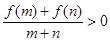
(1)判断函数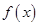 的单调性(不要求证明);
的单调性(不要求证明);
(2)解不等式 ;
;
(3)若 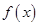
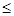
 对于任意的
对于任意的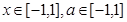 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
已知偶函数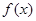 ,对任意
,对任意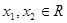 ,恒有
,恒有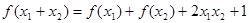 .求:
.求:
(1)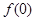 ,
,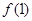 ,
,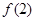 的值;
的值;
(2)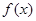 的表达式;
的表达式;
(3) 在
在 上的最值.
上的最值.