已知函数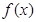 是定义在区间[-1.1]上的奇函数,且
是定义在区间[-1.1]上的奇函数,且 ,对于任意的m,n
,对于任意的m,n [-1,1]有
[-1,1]有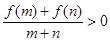
(1)判断函数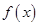 的单调性(不要求证明);
的单调性(不要求证明);
(2)解不等式 ;
;
(3)若 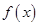
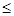
 对于任意的
对于任意的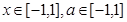 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且面CDE⊥面ABCD. 
求证:CE⊥平面ADE.
正方体ABCD—A1B1C1D1中,E、F、G分别是棱DA、DC、DD1的中点,试找出过正方体的三个顶点且与平面EFG平行的平面,并证明.
如图,已知三棱锥P-ABC中,PA、PB、PC与底面ABC成相等的角,∠CAB=90°,AC=AB,D为BC的中点,E点在PB上,PC∥截面EAD. 
(1)求证:平面PBC⊥底面ABC.
(2)若AB=PB,求AE与底面ABC所成角的正弦值.
如图,已知三棱锥P-ABC中,PA、PB、PC与底面ABC成相等的角,∠CAB=90°,AC=AB,D为BC的中点,E点在PB上,PC∥截面EAD. 
(1)求证:平面PBC⊥底面ABC.
(2)若AB=PB,求AE与底面ABC所成角的正弦值.
已知A、B、C、D、E五点,A、B、C、D共面,B、C、D、E共面,则A、B、C、D、E五点一定共面吗?