( (本小题满分13分)
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2010年1月Q型车的销量为a辆,通过分析预测,若以2010年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:Tn=228a(1.012n-1).(n≤24,n∈N*)
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.
(参考数据:≈1.09,≈8.66)
(本小题满分12分)
编写一个算法流程图,对于函数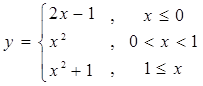 输入x的值,输出相应的函数值,并用基本语句表示此算法。
输入x的值,输出相应的函数值,并用基本语句表示此算法。
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数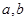 的值;
的值;
| 区间 |
[25,30) |
[30,35) |
[35,40) |
[40,45) |
[45,50] |
| 人数 |
50 |
50 |
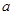 |
150 |
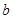 |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
(不计入总分):已知函数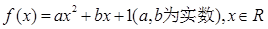 ,设函数
,设函数 ,
,
(3)当a≠0时,求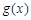 在
在 上的最小值
上的最小值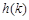 .
.
(本小题满分13分)
已知函数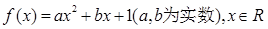 ,设函数
,设函数 ,
,
(1)若 ,且函数
,且函数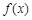 的值域为
的值域为 ,求
,求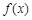 的表达式.
的表达式.
(2)若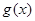 在
在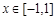 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围.
(本小题满分13分)f(x)为定义在R上的偶函数,但x≥0时,y= f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分。
(1)求函数f(x)在(-∞,0)上的解析式;
(2)求函数f(x)在R上的解析式,并画出函数f(x)的图像;
(3)写出函数f(x)的单调区间