(本小题满分13分)f(x)为定义在R上的偶函数,但x≥0时,y= f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分。
(1)求函数f(x)在(-∞,0)上的解析式;
(2)求函数f(x)在R上的解析式,并画出函数f(x)的图像;
(3)写出函数f(x)的单调区间
(本小题满分12分)
如右图,四边形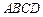 是圆柱
是圆柱 的轴截面,点
的轴截面,点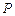 在圆柱
在圆柱 的底面圆周上,
的底面圆周上, 是
是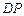 的中点,圆柱
的中点,圆柱 的底面圆的半径
的底面圆的半径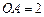 ,侧面积为
,侧面积为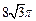 ,
,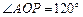 .
.
(Ⅰ)求证: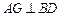 ;
;
(Ⅱ)求二面角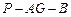 的平面角的余弦值.
的平面角的余弦值.
(本小题满分12分)
计算机考试分理论考试与上机操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中合格的概率分别为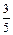 ,
,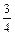 ,
,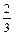 ;在上机操作考试中合格的概率分别为
;在上机操作考试中合格的概率分别为 ,
,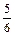 ,
,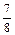 .所有考试是否合格相互之间没有影响.
.所有考试是否合格相互之间没有影响.
(Ⅰ)甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大?
(Ⅱ)求这三人计算机考试都获得“合格证书”的概率;
(Ⅲ)用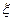 表示甲、乙、丙三人在理论考核中合格人数,求
表示甲、乙、丙三人在理论考核中合格人数,求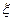 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)
已知数列{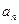 },其前n项和Sn满足Sn+1=2
},其前n项和Sn满足Sn+1=2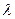 Sn+1(
Sn+1(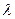 是大于0的常数),且a1=1,a3=4.
是大于0的常数),且a1=1,a3=4.
(Ⅰ)求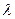 的值;
的值;
(Ⅱ)求数列{an}的通项公式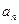 ;
;
24.选修4-5:不等式选讲
若关于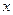 的方程
的方程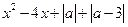 =0有实根
=0有实根
(1)求实数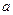 的取值集合
的取值集合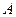
(2)若存在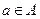 ,使得不等式
,使得不等式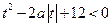 成立,求实数
成立,求实数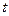 的取值范围。
的取值范围。
.选修4—4:坐标系与参数方程
以平面直角坐标系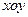 的原点
的原点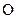 为极点,
为极点,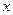 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线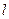 的极坐标方程为
的极坐标方程为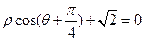 ,曲线
,曲线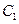 的参数方程为
的参数方程为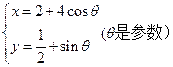
(1)若把曲线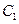 上的横坐标缩短为原来的
上的横坐标缩短为原来的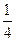 ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线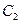 ,
,
求曲线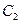 在直角坐标系下的方程
在直角坐标系下的方程
(2)在第(1)问的条件下,判断曲线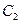 与直线
与直线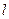 的位置关系,并说明理由;
的位置关系,并说明理由;