
已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为 、
、 ,点E为右准线上的动点,
,点E为右准线上的动点, 的最大值为
的最大值为 .
.
(1)若双曲线的左焦点为 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求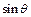 (用
(用 表示);
表示);
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证:
(本小题满分12分)设数列 的前
的前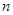 项和为
项和为 ,数列
,数列 的前
的前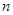 项和为
项和为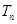 ,且满足
,且满足 .
.
(1)求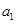 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)记  ,求证:
,求证: .
.
(本小题满分12分)设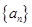 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且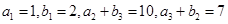 .
.
(1)求数列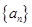 ,
, 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为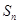 ,记
,记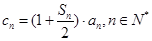 ,求数列
,求数列 的前
的前 项和
项和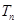 .
.
(本小题满分12分)某厂生产某种产品的年固定成本为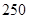 万元,每生产
万元,每生产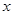 (
(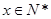 )千件,需另投入成本为
)千件,需另投入成本为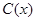 ,当年产量不足
,当年产量不足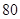 千件时,
千件时,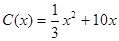 (万元);当年产量不小于
(万元);当年产量不小于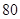 千件时,
千件时,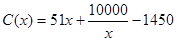 (万元).通过市场分析,若每件售价为
(万元).通过市场分析,若每件售价为 元时,该厂年内生产该商品能全部销售完.
元时,该厂年内生产该商品能全部销售完.
(1)写出年利润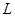 (万元)关于年产量
(万元)关于年产量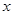 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(本小题满分12分)在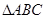 中,内角
中,内角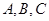 的对边分别为
的对边分别为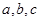 ,且
,且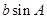 =
=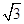
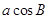 .
.
(1)求角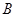 的大小;
的大小;
(2)若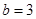 ,求
,求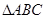 的面积
的面积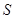 的最大值.
的最大值.
(本小题满分12分)已知命题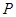 :对
:对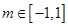 ,不等式
,不等式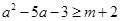 恒成立;命题
恒成立;命题 有解,若
有解,若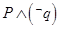 为真,求实数
为真,求实数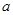 的取值范围.
的取值范围.