袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
(本题满分13分)已知函数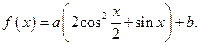
(1)当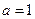 时,求函数的单调递增区间;(2)当
时,求函数的单调递增区间;(2)当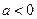 时,函数
时,函数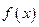 的值域是
的值域是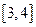 ,求
,求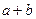 的值
的值
(本题满分12分).如图:平面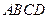
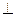 平面
平面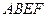 ,
,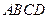 是正方形,
是正方形,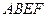 矩形,且
矩形,且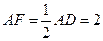 ,
,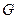 是
是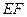 的中点。
的中点。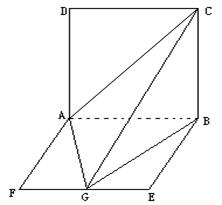
(1)求证平面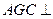 平面
平面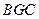 ;(2)求四面体
;(2)求四面体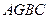 的体积。
的体积。
(本题满分12分)中心在原点的椭圆与抛物线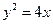 有一个公共焦点,且其离心率是双曲线
有一个公共焦点,且其离心率是双曲线 的离心率的倒数,
的离心率的倒数,
(1)求椭圆方程。(2)若(1,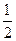 )是直线
)是直线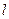 被椭圆截得的线段的中点,求直线
被椭圆截得的线段的中点,求直线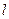 的方程。
的方程。
(本题满分12分)已知点M在X轴上,点N在Y轴上,且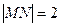 ,点P为线段MN的中点。
,点P为线段MN的中点。
(1) 求点P的轨迹方程。
(2)若直线 与上述轨迹交于A.B两点,且
与上述轨迹交于A.B两点,且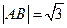 ,求:
,求: 的值。
的值。
(本小题满分12分)如图,在三棱锥 中,
中,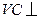 底面
底面 ,
, ,
,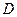 是
是 的中点,且
的中点,且 ,
,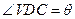
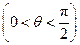 .
.
(1)求证:平面 平面
平面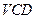 ;(2)当角
;(2)当角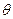 变化时,求直线
变化时,求直线 与平面
与平面 所成的角
所成的角
的取值范围。