(示范性高中做)
某公司计划在甲、乙两个仓储基地储存总量不超过300吨的一种紧缺原材料,总费用不超过9万元,此种原材料在甲、乙两个仓储基地的储存费用分别为 元/吨和200元/吨,假定甲、乙两个仓储基地储存的此种原材料每吨能给公司带来的收益分别为0.3万元和0.2万元
元/吨和200元/吨,假定甲、乙两个仓储基地储存的此种原材料每吨能给公司带来的收益分别为0.3万元和0.2万元 问该公司如何分配在甲、乙两个仓储基地的储存量,才能使公司的收益最大,最大收益是多少万元?
问该公司如何分配在甲、乙两个仓储基地的储存量,才能使公司的收益最大,最大收益是多少万元?
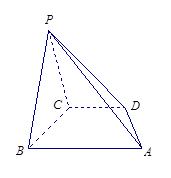
在四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形,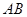 ∥
∥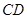 ,∠
,∠ ,
,  ,平面
,平面 ⊥平面
⊥平面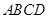 .
.
(1)求证: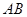 ⊥平面
⊥平面 ;
;
(2)求平面 和平面
和平面 所成二面角(小于
所成二面角(小于 )的大小;
)的大小;
(3)在棱 上是否存在点
上是否存在点 使得
使得 ∥平面
∥平面 ?若存在,求
?若存在,求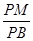 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
有甲,乙两个盒子,甲盒中装有2个小球,乙盒中装有3个小球,每次随机选取一个盒子并从中取出一个小球
(1)当甲盒中的球被取完时,求乙盒中恰剩下1个球的概率;
(2)当第一次取完一个盒子中的球时,另一个盒子恰剩下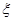 个球,求
个球,求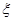 的分布列及期望
的分布列及期望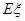 。
。
已知函数 ,
,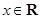
(1)求函数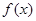 的最小正周期;(2)若
的最小正周期;(2)若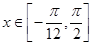 ,求函数
,求函数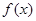 的值域
的值域
已知函数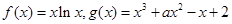
(1)如果函数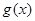 的单调减区间为
的单调减区间为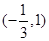 ,求函数
,求函数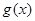 的解析式;
的解析式;
(2)在(1)的条件下,求函数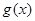 的图像过点
的图像过点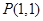 的切线方程;
的切线方程;
(3)证明:对任意的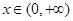 ,不等式
,不等式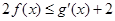 恒成立,求实数
恒成立,求实数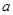 的取值范围。
的取值范围。
已知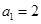 ,点
,点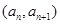 在函数
在函数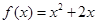 的图象上,其中
的图象上,其中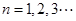
(1)求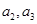 ;
;
(2)证明数列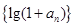 是等比数列;
是等比数列;
(3)设 ,求
,求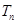 及数列
及数列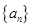 的通项
的通项