有甲,乙两个盒子,甲盒中装有2个小球,乙盒中装有3个小球,每次随机选取一个盒子并从中取出一个小球
(1)当甲盒中的球被取完时,求乙盒中恰剩下1个球的概率;
(2)当第一次取完一个盒子中的球时,另一个盒子恰剩下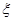 个球,求
个球,求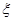 的分布列及期望
的分布列及期望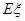 。
。
(本小题满分12分)已知向量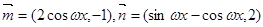
 ,
,
函数 ,若函数
,若函数 的图象的两个相邻对称中心的距离为
的图象的两个相邻对称中心的距离为 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)若将函数 的图象先向左平移
的图象先向左平移 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的 倍,得到函数
倍,得到函数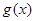 的图象,当
的图象,当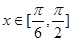 时,求函数
时,求函数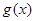 的值域.
的值域.
选修4-5: 不等式选讲
已知函数 f (x)=" |x" - 2|,g(x)=" -|x" + 3| +m.
(Ⅰ)若关于x的不等式 g(x)≥0的解集为 [-5, -1], 求实数m的值;
(Ⅱ)若 f (x)的图象恒在 g(x)图象的上方, 求实数m的取值范围.
选修4-4: 坐标系与参数方程
在极坐标系中, 已知圆C的圆心C(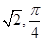 ), 半径r =
), 半径r = .
.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)若 α ∈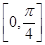 , 直线
, 直线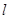 的参数方程为
的参数方程为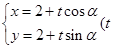 为参数), 直线
为参数), 直线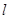 交圆C于A、 B两点, 求弦长|AB|的取值范围.
交圆C于A、 B两点, 求弦长|AB|的取值范围.
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C, D
两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.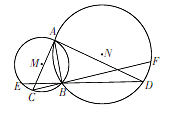
(Ⅰ)求AB的长;
(Ⅱ)求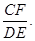
己知函数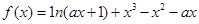 .
.
(Ⅰ)若 x = 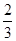 为 f (x)的极值点, 求实数a的值;
为 f (x)的极值点, 求实数a的值;
(Ⅱ)若 y =" f" (x)在[l, +∞)上为增函数, 求实数a的取值范围;
(Ⅲ)若a=-1时, 方程 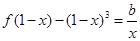 有实根, 求实数b的取值范围.
有实根, 求实数b的取值范围.