(本小题满分14分)已知函数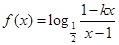 为奇函数.
为奇函数.
(1)求常数k的值;
(2)若 ,试比较
,试比较 与
与 的大小;
的大小;
(3)若函数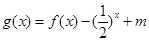 ,且
,且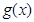 在区间
在区间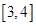 上没有零点,求实数m的取值范围.
上没有零点,求实数m的取值范围.
(本小题满分12分)设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为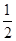 的椭圆记作C2
的椭圆记作C2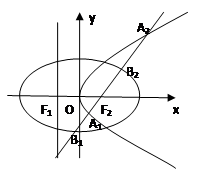
(1)求椭圆的标准方程;
(2)直线L经过椭圆C2的右焦点F2,与抛物线C1交于A1,A2两点,与椭圆C2交于B1,B2两点。当以B1B2为直径的圆经过F1时,求|A1A2|长。
(3)若M是椭圆上的动点,以M为圆心,MF2为半径作圆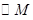 ,是否存在定圆
,是否存在定圆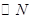 ,使得
,使得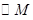 与
与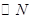 恒相切?若存在,求出
恒相切?若存在,求出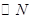 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
(本小题满分12分)如图,在四棱台ABCD-A1B1C1D1中,DD1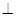 平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,
平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,

(1)证明:BB1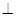 AC;
AC;
(2)若AB=2,且二面角A1-AB-C大小为60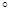 ,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式:
,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式: ,R是球半径)
,R是球半径)
(本小题满分12分)
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格。
(1)用样本估计总体,请根据茎叶图对甲乙两个班级的成绩进行比较。
(2)求从甲班10名学生和乙班10名学生中各抽取一人,已知有人及格的条件下乙班同学不及格的概率;
(3)从甲班10人中抽取一人,乙班10人中抽取二人,三人中及格人数记为X,求X的分布列和期望。
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合;
的取值集合;
(Ⅱ)已知 中,角A,B,C的对边分别为a,b,c若
中,角A,B,C的对边分别为a,b,c若 b+c=2。求实数a的取值范围。
b+c=2。求实数a的取值范围。
已知无穷数列 的各项均为正整数,
的各项均为正整数, 为数列
为数列 的前
的前 项和.
项和.
(Ⅰ)若数列 是等差数列,且对任意正整数
是等差数列,且对任意正整数 都有
都有 成立,求数列
成立,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数 ,从集合
,从集合 中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与
中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与 一起恰好是1至
一起恰好是1至 全体正整数组成的集合.
全体正整数组成的集合.
(ⅰ)求 的值;(ⅱ)求数列
的值;(ⅱ)求数列 的通项公式.
的通项公式.