(本小题满分12分)设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为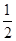 的椭圆记作C2
的椭圆记作C2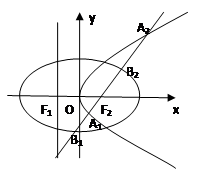
(1)求椭圆的标准方程;
(2)直线L经过椭圆C2的右焦点F2,与抛物线C1交于A1,A2两点,与椭圆C2交于B1,B2两点。当以B1B2为直径的圆经过F1时,求|A1A2|长。
(3)若M是椭圆上的动点,以M为圆心,MF2为半径作圆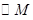 ,是否存在定圆
,是否存在定圆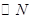 ,使得
,使得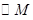 与
与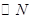 恒相切?若存在,求出
恒相切?若存在,求出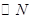 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
如图所示,在平面直角坐标系xOy中,一次函数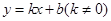 的图象与反比例函数
的图象与反比例函数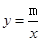 的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=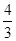 ,求△AOB的面积.
,求△AOB的面积.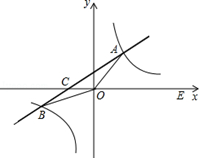
先化简,再求值: ,其中
,其中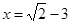 .
.
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出 的取值范围.
的取值范围.
已知关于x的一元二次方程 .
.
(1)若此方程有两个不相等的实数根,求实数k的取值范围;
(2)已知x=3是此方程的一个根,求方程的另一个根及k的值;
(3)当Rt△ABC的斜边长C= ,且两条直角边A和B恰好是这个方程的两个根时,求Rt△ABC的面积.
,且两条直角边A和B恰好是这个方程的两个根时,求Rt△ABC的面积.