为了迎接省运会，为了降低能源损耗，鹰潭市体育馆的外
墙需要建造隔热层．体育馆要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度
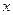（单位：cm）满足关系：
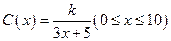，若不建隔热层，每年能源消耗费用为8万元．设
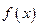为隔热层建造费用与20年的能源消
耗费用之和．
（1）求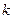
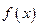的值及的表达式；
（2）隔热层修建多厚时，总费用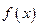达到最小，并求最小值
如图，已知椭圆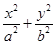
（a＞b＞0）的离心率
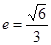，过点A（0，-b）和B（a，0）的直线与原点的距离为
．
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y＝kx＋2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点?请说明理由.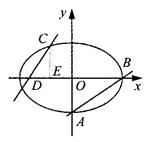
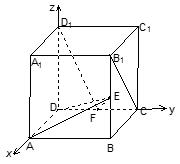
在正方体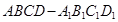
中，如图Ｅ、Ｆ分别是 
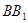，CD的中点，
（1）求证：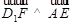
；
（2）求
. 
已知：等差数列{
}中，
=14，前10项和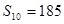
.
（Ⅰ）求；
（Ⅱ）将{}中的第2项，第4项，…，第
项按原来的顺序排成一个新数列，求此数列的前
项和
.
抛物线的顶点在原点，它的准线过双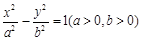
曲线的一个焦点，并与
双曲线的实轴垂直，已知抛物线与双曲线的交点为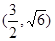
，求抛物线的方程和双曲线的方程.
已知关于x的一元二次方程 (m∈Z)
① mx2－4x＋4＝0,
② x2－4mx＋4m2－4m－5＝0，求方程①和②都有整数解的充要条件.