(本小题满分12分)
设数列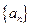 为等差数列,且
为等差数列,且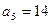 ,
,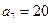 ,数列
,数列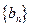 的前
的前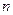 项和为
项和为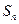 ,
,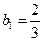 且
且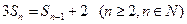 ;
;
(Ⅰ)求数列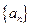 ,
,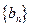 的通项公式;
的通项公式;
(Ⅱ)若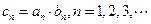 ,
,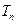 为数列
为数列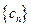 的前
的前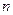 项和. 求证:
项和. 求证: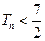 .
.
如图,
已知正三棱柱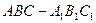 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱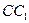 的中点,平面ABD和平面
的中点,平面ABD和平面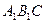 的交线为MN.
的交线为MN.
(Ⅰ)试证明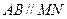 ;
;
(Ⅱ)若直线AD与侧面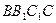 所成的角为
所成的角为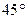 ,试求二面角
,试求二面角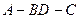 的大小.
的大小.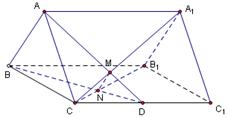
袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.
(Ⅰ)若有放回地摸出4个球,求取出的红球数不小于黑球数的概率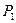 ;
;
(Ⅱ)若无放回地摸出4个球,
①求取出的红球数ξ的概率分布列和数学期望;
②求取出的红球数不小于黑球数的概率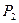 ,并比较
,并比较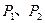 的大小.
的大小.
设平面上向量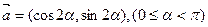 ,
,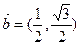 ,
,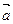 与
与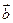 不共线,
不共线,
(Ⅰ)证明向量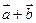 与
与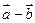 垂直;
垂直;
(Ⅱ)若两个向量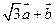 与
与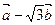 的模相等,试求角
的模相等,试求角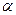 .
.
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且 .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求 的值.
的值.
 |
在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
(1)求证:AD⊥平面BC C1 B1;
(2)设E是B1C1上的一点,当 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.