(本小题满分12分)设数列 和
和 满足:
满足: ,数列
,数列 是等差数列,
是等差数列, 为数列
为数列 的前
的前 项和,且
项和,且 ,
,
(I)求数列 和
和 的通项公式;
的通项公式;
(II)是否存在 ,使
,使 ?若存在,求出
?若存在,求出 ,若不存在,说明理由。
,若不存在,说明理由。
(本小题满分12分)已知函数 ,
,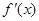 是
是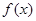 的导函数.
的导函数.
(1)求函数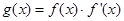 的最小值及相应的
的最小值及相应的 值的集合;
值的集合;
(2)若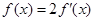 ,求
,求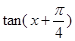 的值.
的值.
(本题10分)已知函数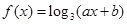 的图象经过点
的图象经过点 和
和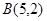 ,记
,记
(1)求数列 的通项公式;
的通项公式;
(2)设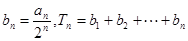 ,若
,若 ,求
,求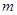 的最小值;
的最小值;
(3)求使不等式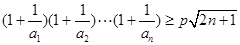 对一切
对一切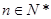 均成立的最大实数
均成立的最大实数 .
.
(本题8分)已知抛物线C: 和直线L:y =-2,直线L与y轴的交点D(0,-2),过点Q(0,2)的直线交抛物线C于A、B两点,与直线L交于点P.
和直线L:y =-2,直线L与y轴的交点D(0,-2),过点Q(0,2)的直线交抛物线C于A、B两点,与直线L交于点P.
(1)记 的面积为S,求S的取值范围;
的面积为S,求S的取值范围;
(2)设 ,
, ,求
,求 的值。
的值。
(本题8分)已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求异面直线DE与AB所成角的余弦值;
(2)求二面角A-ED-B的正弦值;
(3)求此几何体的体积V的大小。
(本题8分)已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值;
(Ⅱ)设△ABC的对边分别为 ,若
,若 =
= ,
, ,
, ,求
,求 的值.
的值.