(本小题满分14分)已知等差数列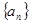 的前
的前 项和为
项和为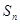 ,
,  .
.
(1)求数列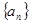 的通项公式;
的通项公式;
(2)当 为何值时,
为何值时, 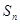 取得最小值.
取得最小值.
在R上定义运算 ,记
,记 ,
,
(1)若 在x=1处有极值
在x=1处有极值 ,求b, c的值;
,求b, c的值;
(2)求曲线 上斜率为c的切线与该曲线的公共点;
上斜率为c的切线与该曲线的公共点;
(3)记 的最大值为M,若
的最大值为M,若 对任意b, c恒成立,求k的最大值。
对任意b, c恒成立,求k的最大值。
设函数 。
。
(1)求 的单调区间;
的单调区间;
(2)若 ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若方程 在区间[0, 2] 恰有两个不等实根,求a的取值范围。
在区间[0, 2] 恰有两个不等实根,求a的取值范围。
ΔABC中,角A, B, C所对的边分别为a, b, c,且 。
。
(1)求 的值;(2)若
的值;(2)若 及ΔABC的面积。
及ΔABC的面积。
对定义在[0, 1]上并且满足下列两个条件的函数 称为G函数。①对任意的
称为G函数。①对任意的 ,②
,② 成立。已知
成立。已知 是定义在[0, 1]上的函数。
是定义在[0, 1]上的函数。
(1)问 是否为G函数,说明理由;
是否为G函数,说明理由;
(2)若 是G函数,求实数m取值的范围。
是G函数,求实数m取值的范围。
已知 。
。
求下列各式的值: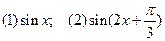 。
。