设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的 ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f( ),则(0,
),则(0, )为含峰区间:若f(
)为含峰区间:若f( )
) f(
f( ),则
),则 为含峰区间:
为含峰区间:
(II)对给定的r(0<r<0.5),证明:存在 ∈(0,1),满足
∈(0,1),满足 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:
(III)选取 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 与
与 或
或 与
与 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, )的情况下,试确定的值
)的情况下,试确定的值 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
(本小题满分14分)设数列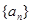 的前
的前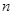 项和为
项和为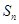 ,点
,点 在直线
在直线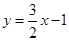 上.
上.
(Ⅰ)求数列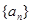 的通项公式;
的通项公式;
(Ⅱ)在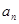 与
与 之间插入
之间插入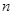 个数,使这
个数,使这 个数组成公差为
个数组成公差为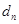 的等差数列,求数列
的等差数列,求数列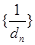 的前
的前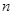 项和
项和 ,并求使
,并求使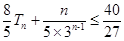 成立的正整数
成立的正整数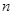 的最大值.
的最大值.
已知 中,
中, 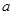 ,
,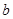 ,
, 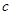 分别为角
分别为角  ,
, ,
, 所对的边,
所对的边, .
.
(Ⅰ)求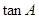 的值;
的值;
(Ⅱ)若 的面积为
的面积为 ,
,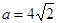 ,求
,求 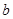 、
、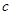 的长.
的长.
(本小题满分14分)已知函数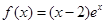 和
和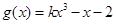 .
.
(Ⅰ)若函数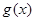 在区间
在区间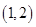 不单调,求实数
不单调,求实数 的取值范围;
的取值范围;
(Ⅱ)当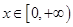 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(本小题满分15分)已知椭圆 的左右焦点
的左右焦点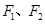 ,离心率为
,离心率为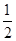 ,双曲线方程为
,双曲线方程为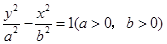 ,直线
,直线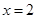 与双曲线的交点为
与双曲线的交点为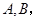 且
且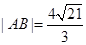 .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点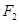 的直线
的直线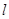 与椭圆交于
与椭圆交于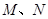 两点,交双曲线与
两点,交双曲线与 两点,当
两点,当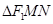 (
( 为椭圆的左焦点)的内切圆的面积取最大值时,求
为椭圆的左焦点)的内切圆的面积取最大值时,求 的面积.
的面积.
(本小题满分15分)如图,在三棱锥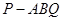 中,
中,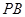 ⊥平面
⊥平面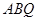 ,
,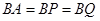 ,
, ,
,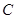 ,
,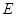 ,
, 分别是
分别是 ,
,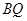 ,
,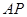 ,
, 的中点,
的中点, ,
,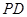 与
与 交于点
交于点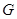 ,
, 与
与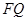 交于点
交于点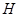 ,连结
,连结 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求平面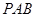 与平面
与平面 所成角的正弦值.
所成角的正弦值.