已知双曲线 的焦点与椭圆
的焦点与椭圆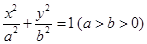 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
, 是椭圆上的的动点.
是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: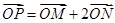 ,直线
,直线 与
与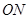 的斜率之积为
的斜率之积为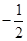 ,求证:存在定点
,求证:存在定点 ,
,
使得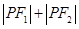 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若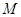 在第一象限,且点
在第一象限,且点 关于原点对称,点
关于原点对称,点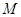 在
在 轴的射影为
轴的射影为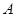 ,连接
,连接 并延长交椭圆于
并延长交椭圆于
点 ,求证:以
,求证:以 为直径的圆经过点
为直径的圆经过点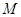 .
.
(本小题12分)
已知 ABC的顶点C(5,1),AC边上的中线BM所在直线方程为
ABC的顶点C(5,1),AC边上的中线BM所在直线方程为 ,BC边上的高AH所在直线方程为
,BC边上的高AH所在直线方程为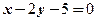 ,求:
,求:
(1)顶点B的坐标;
(2)直线AC的方程.
(本小题12分)
如图,三棱柱ABC-A1B1C1的 侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
侧棱与底面垂直,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
(1)求证:AC⊥B1C;
(2)求证:AC 1∥平面CDB1.
(本小题10分)
已知甲、乙两地相距150km,某人开汽车以6 0km/h的速度从
0km/h的速度从 甲地到达乙地,在乙地停留1小时后再以50km/h的速度返回甲地,把汽车离开甲地的距离s表示为时间t(从甲地出发时开始)的函数,求此函数表达式.
甲地到达乙地,在乙地停留1小时后再以50km/h的速度返回甲地,把汽车离开甲地的距离s表示为时间t(从甲地出发时开始)的函数,求此函数表达式.
(本小题10分)
已知集合 全集
全集
(1)求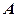 ∪
∪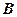 、(
、(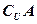 )∩
)∩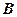 ;
;
(2)若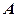 ∩
∩ ,求实数
,求实数 的取值范围。
的取值范围。
(本小题满分12分)
已知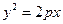
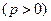 ,过点
,过点 作直线与抛物线交于两点,若两点纵坐标之积为
作直线与抛物线交于两点,若两点纵坐标之积为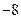 .
.
(1)求抛物线方程;
(2)斜率为 的直线不经过点
的直线不经过点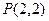 且与抛物线交于
且与抛物线交于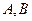
(Ⅰ)求直线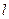 在
在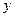 轴上截距
轴上截距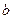 的取值范围;
的取值范围;
(Ⅱ)若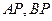 分别与抛物线交于另一点
分别与抛物线交于另一点 ,证明:
,证明: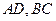 交于一定点
交于一定点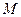 .
.