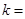(本小题共10分)在直三棱柱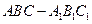 中,
中, ,
, ,求
,求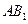 与侧面
与侧面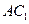 所成的角。
所成的角。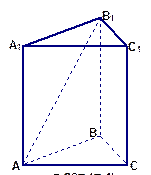
已知顶点在原点,焦点在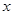 轴上的抛物线被直线
轴上的抛物线被直线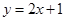 截得的弦长为
截得的弦长为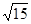 ,(1)求抛物线的方程;(2)若抛物线与直线
,(1)求抛物线的方程;(2)若抛物线与直线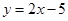 无公共点,试在抛物线上求一点,使这点到直线
无公共点,试在抛物线上求一点,使这点到直线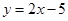 的距离最短。
的距离最短。
已知四棱锥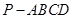 的底面为直角梯形,
的底面为直角梯形,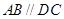 ,
, 底面
底面 ,且
,且 ,
,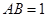 ,
,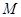 是
是 的中点。
的中点。
(Ⅰ)证明:面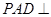 面
面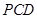 ;
;
(Ⅱ)求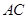 与
与 所成的角的余弦值;
所成的角的余弦值;
(Ⅲ)求面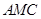 与面
与面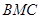 所成二面角的余弦值。
所成二面角的余弦值。
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求直线BC与平面APB所成角的正弦值
(Ⅲ)求点C到平面APB的距离.
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
已知椭圆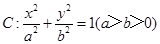 的离心率为
的离心率为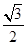 ,过右焦点
,过右焦点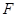 且斜率为
且斜率为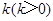 的直线与
的直线与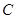 相交于
相交于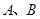 两点.若
两点.若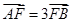 ,则
,则