某家庭进行理财投资,根据长期收益率市场预测投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).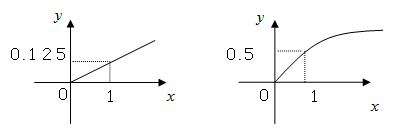
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:投资债券类产品和投资股票分别多少万元,能使投资获得最大收益,其最大收益是多少万元?
已知数列 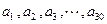 ,其中
,其中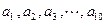 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为  的等差数列;
的等差数列;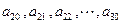 是公差为
是公差为  的等差数列(
的等差数列( ).
).
(1)若 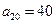 ,求
,求  ;
;
(2)试写出 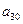 关于
关于  的关系式;
的关系式;
(3)续写已知数列,使得 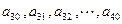 是公差为
是公差为 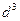 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题,并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题,并进行研究,你能得到什么样的结论?
在复平面上,设点A、B、C 对应的复数分别为  。过A、B、C 三个点做平行四边形。 求第四个顶点D的坐标及此平行四边形的对角线的长。
。过A、B、C 三个点做平行四边形。 求第四个顶点D的坐标及此平行四边形的对角线的长。
已知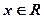 ,
, ,
, 。求证
。求证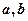 中至少有一个不小于0。
中至少有一个不小于0。
(本小题满分15分)
如图,已知抛物线 的准线为
的准线为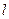 ,
, 为
为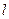 上的一个动点,过点
上的一个动点,过点 作抛物
作抛物
线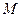 的两条切线,切点分别为
的两条切线,切点分别为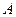 ,
, ,再分别过
,再分别过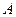 ,
, 两点作
两点作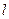 的垂线,垂足分别为
的垂线,垂足分别为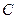 ,
, .
.
(1)求证:直线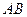 必经过
必经过 轴上的一个定点
轴上的一个定点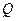 ,并写出点
,并写出点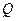 的坐标;
的坐标;
(2)若 ,
, ,
, 的面积依次构成等差数列,求此时点
的面积依次构成等差数列,求此时点 的坐标.
的坐标.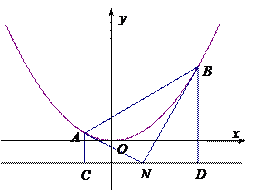
已知函数 是不同时为零的常数),其导函数为
是不同时为零的常数),其导函数为 。
。
(1)当a= 时,若存在
时,若存在 ,使得
,使得 >0成立,求b的取值范围;
>0成立,求b的取值范围;
(2)求证:函数y= 在(-1,0)内至少存在一个零点;
在(-1,0)内至少存在一个零点;
(3)若函数f(x)为奇函数,且在x=1处的切线垂直于直线x+2y-3="0," 关于x的方程 在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。
在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围。