设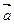 、
、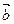 是两个不共线的非零向量(
是两个不共线的非零向量(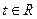 ).
).
(I)记 ,那么当实数t为何值时,A、B、C三点共线?
,那么当实数t为何值时,A、B、C三点共线?
(II)若 ,那么实数x为何值时
,那么实数x为何值时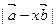 的值最小?
的值最小?
(本小题满分14分)
在四棱锥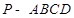 中,底面
中,底面 是直角梯形,
是直角梯形, ∥
∥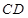 ,
,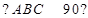 ,
, ,平面
,平面 平面
平面 .
.
(Ⅰ)求证: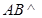 平面
平面 ;
;
(Ⅱ)求平面 和平面
和平面 所成二面角(小于
所成二面角(小于 )的大小;
)的大小;
(Ⅲ)在棱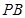 上是否存在点
上是否存在点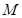 使得
使得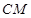 ∥平面
∥平面 ?若存在,求
?若存在,求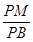 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 
(本小题满分13分)
为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,
,  ,
, .
.
(Ⅰ)求 及
及 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的面积.
的面积.
已知椭圆 经过点
经过点 ,
, 为坐标原点,平行于
为坐标原点,平行于 的直线
的直线 在
在 轴上的截距为
轴上的截距为
 .
.
(1)当 时,判断直线
时,判断直线 与椭圆的位置关系(写出结论,不需证明);
与椭圆的位置关系(写出结论,不需证明);
(2)当 时,
时, 为椭圆上的动点,求点
为椭圆上的动点,求点 到直线
到直线 距离的最小值;
距离的最小值;
(3)如图,当 交椭圆于
交椭圆于 、
、 两个不同点时,求证:直线
两个不同点时,求证:直线 、
、 与
与 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
如图, 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, 与平面
与平面 所成角是
所成角是 ,点
,点 是
是 的中点,点
的中点,点 在矩形
在矩形 的边
的边 上移动.
上移动.
(1)证明:无论点 在边
在边 的何处,都有
的何处,都有 ;
;
(2)当 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.