(本小题满分12分)
在 中,已知
中,已知 ,且
,且 .
.
(Ⅰ)求 的大小。
的大小。
(Ⅱ)证明 是等边三角形
是等边三角形
k
已知函数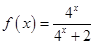 .
.
(Ⅰ)求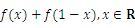 的值;
的值;
(Ⅱ)若数列{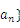 ,
,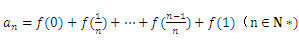 ,求数列{
,求数列{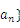 的通项公式;
的通项公式;
(Ⅲ)若数列{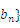 满足
满足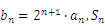 是数列{
是数列{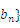 的前n项和,是否存在正实数k,使不等式
的前n项和,是否存在正实数k,使不等式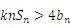 对于一切的
对于一切的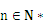 恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
已知数列 满足:
满足: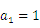 ,
,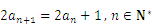 .数列
.数列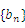 的前n项和为
的前n项和为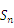 ,
,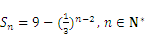 .
.
(1)求数列 ,
,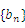 的通项公式;
的通项公式;
(2)设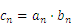 ,
,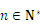 .求数列
.求数列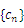 的前项和
的前项和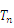 .
.
2009年推出一款新型家用轿车,购买时费用为14.4万元,每年应交付保险费、 养路费及汽油费共0.7万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(1)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
设向量a=(4cosα,sinα),b=(sinβ,4cosβ),c=(cosβ,-4sinβ),
(1)若a与b-2c垂直,求tan(α+β)的值;
(2)求|b+c|的最大值.
已知函数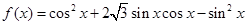
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在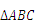 中,A、B、C分别为三边
中,A、B、C分别为三边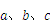 所对的角,若a=
所对的角,若a=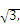 f(A)=1,求
f(A)=1,求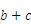 的最大值.
的最大值.