(本小题满分10分)
四棱锥P-ABCD中,底面ABCD是正方形,
边长为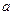 ,PD=
,PD=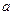 ,PD⊥平面ABCD
,PD⊥平面ABCD
(1)求证: AC⊥PB ;
(2)求二面角A-PB-D的大小;
(3)求四棱锥外接球的半径.
(4)在这个四棱锥中放入一个球,求球的最大半径;

(本题满分16分,第(1)小题6分,第(2)小题10分)
已知圆 ,点
,点 ,点
,点 在圆
在圆 上运动,
上运动, 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(1)求动点 的轨迹
的轨迹 方程;
方程;
(2)过点 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线 于
于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以 为直径的圆恒过这个点?若存在,请求出点
为直径的圆恒过这个点?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题满分15分,第(1)小题6分,第(2)小题9分)
如图所示,某市拟在长为 道路
道路 的一侧修建一条运动赛道,赛道的前一部分为曲线段
的一侧修建一条运动赛道,赛道的前一部分为曲线段 ,该曲线段为函数
,该曲线段为函数
 的图像,且图像的最高点为
的图像,且图像的最高点为 ,赛道的后一部分为折线段
,赛道的后一部分为折线段 ,且
,且 .
.
(1)求 、
、 两点间的直线距离;
两点间的直线距离;
(2)求折线段赛道 长度的最大值.
长度的最大值.
(本题满分14分,第(1)、(2)小题各3分;第(3)、(4)小题各4分)
请你指出函数
 的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
(1)当 时,等式
时,等式 恒成立;
恒成立;
(2)若 ,则一定有
,则一定有 ;
;
(3)若 ,方程
,方程 有两个不相等的实数解;
有两个不相等的实数解;
(4)函数 在
在 上有三个零点.
上有三个零点.
(本题满分12分,第(1)小题5分,第(2)小题7分)
如图, 是圆柱体
是圆柱体 的一条母线,已知
的一条母线,已知 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 上不与点
上不与点 重合的任意一点,
重合的任意一点, ,
, ,
, .
.
(1)求直线 与直线
与直线 所成角的大小;
所成角的大小;
(2)将四面体 绕母线
绕母线 旋转一周,求
旋转一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
我们把一系列向量 按次序排成一列,称之为向量列,记作
按次序排成一列,称之为向量列,记作 ,已知向量列
,已知向量列 满足:
满足: ,
,
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)设 ,问数列
,问数列 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由;
中是否存在最小项?若存在,求出最小项;若不存在,请说明理由;
(3)设 表示向量
表示向量 与
与 间的夹角,若
间的夹角,若 ,对于任意正整数
,对于任意正整数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的范围.
的范围.