(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且二面角A-DC-E为直二面角。
(1)求证:CD⊥DE; (2)求AE与面DEC所成的角.
(本小题共10分)
已知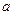 、
、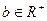 ,求证:
,求证: .
.
(本小题满分12分)
已知二次函数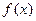 满足
满足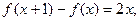 且
且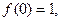
(1)求二次函数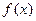 的解析式。
的解析式。
(2)在区间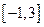 上,
上,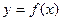 的图像恒在
的图像恒在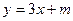 的图像的上方。
的图像的上方。
求实数m的取值范围。
(本小题满分12分)
已知直线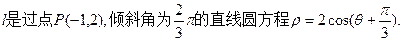
(I)求直线l的参数方程;
(II)设直线l与圆相交于M、N两点,求|PM|·|PN|的值。
(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
乙厂 乙厂
乙厂
(1)、试分别估计两个分厂生产的零件的优质品率;
(2)、由以上统计数据填下面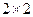 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| 甲 厂 |
乙 厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合计 |
附: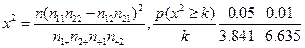
(本小题满分12分)
某村计划建造一个室内面积为800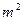 的矩形蔬菜温室,在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积为多少?
的矩形蔬菜温室,在温室内沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积为多少?