某单位设计的两种密封玻璃窗如图所示：图1是单层玻璃，厚度为8 mm；图2是双层中空玻璃，厚度均为4 mm，中间留有厚度为
的空气隔层．根据热传导知识，对于厚度为
的均匀介质，两侧的温度差为
，单位时间内，在单位面积上通过的热量
，其中
为热传导系数．假定单位时间内，在单位面积上通过每一层玻璃及空气隔层的热量相等．（注：玻璃的热传导系数为
，空气的热传导系数为
．）
（1）设室内，室外温度均分别为
，
，内层玻璃外侧温度为
，外层玻璃内侧温度为
，且
．试分别求出单层玻璃和双层中空玻璃单位时间内，在单位面积上通过的热量（结果用，及表示）；
（2）为使双层中空玻璃单位时间内，在单位面积上通过的热量只有单层玻璃的4%，应如何设计的大小？
设函数
．
（１）解不等式
（２）若关于
的不等式
的解集不是空集，试求实数
的取值范围.
已知曲线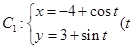
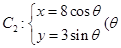为参数），
为参数）.
（1）化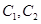
的方程为普通方程
（2）若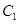
上的点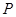
对应的参数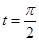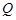为
，
为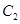
上的动点，求
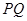中点
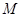到直线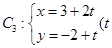
为参数）距离的最小值.
如图，在△
中，
是
的中点，
是
的中点，
的延长线交
于
.
（Ⅰ）求
的值；
（Ⅱ）若△
的面积为
， 四边形
的面积为
，求
的值．
已知函数
（常数
）.
（Ⅰ）求
的单调区间；
（Ⅱ）设
如果对于的图象上两点
，存在
，使得的图象在
处的切线
∥
，求证：
.
已知
分别为椭圆
的上下焦点，其中
也是抛物线
的焦点，点
是
与
在第二象限的交点，且
.
（1）求椭圆的方程；
（2）已知点
和圆
，过点
的动直线
与圆
相交于不同的两
点
，在线段
上取一点
,满足
且
.
求证：点总在某定直线上.