设函数 .
.
(1)解不等式
(2)若关于 的不等式
的不等式 的解集不是空集,试求实数
的解集不是空集,试求实数 的取值范围.
的取值范围.
已知抛物线y=x2上的两点A、B满足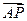 =l
=l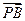 ,l>0,其中点P坐标为(0,1),
,l>0,其中点P坐标为(0,1), =
= +
+ ,O为坐标原点.
,O为坐标原点.
(I)求四边形OAMB的面积的最小值;
(II)求点M的轨迹方程.
设A,B分别是直线 和
和 上的两个动点,并且
上的两个动点,并且 ,动点P满足
,动点P满足 .记动点P的轨迹为C.
.记动点P的轨迹为C.
(I)求轨迹C的方程;
(II)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且 ,求实数
,求实数 的取值范围.
的取值范围.
已知A.B是椭圆 上两点,O是坐标原点,定点
上两点,O是坐标原点,定点 ,向量
,向量 .
. 在向量
在向量 方向上的投影分别是m.n ,且
方向上的投影分别是m.n ,且 7mn ,动点P满足
7mn ,动点P满足
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)设过点E的直线l与C交于两个不同的点M.N,求 的取值范围。
的取值范围。
已知点P与定点F 的距离和它到定直线l:
的距离和它到定直线l: 的距离之比是1 : 2.
的距离之比是1 : 2.
(1)求点P的轨迹C方程;
(2)过点F的直线交曲线C于A, B两点, A, B在l上的射影分别为M, N.
求证AN与BM的公共点在x轴上.
已知双曲线G的中心在原点,它的渐近线与圆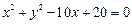 相切,过点P(-4,0)作斜率为
相切,过点P(-4,0)作斜率为 的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足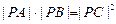
(1)求双曲线G的渐近线方程
(2)求双曲线G的方程
(3)椭圆S的中心在原点,它的短轴是G的实轴,如果S中垂直于l的平行弦的中点轨迹恰好是G的渐近线截在S内的部分,求椭圆S的方程。