某产品具有一定的时效性，在这个时效期内，由市场调查可知，在不做广告宣传且每件获利a元的前提下，可卖出b件；若做广告宣传，广告费为n千元比广告费为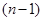
千元时多卖出
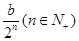件。
（1）试写出销售量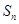
与n的函数关系式；
（2）当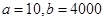
时，厂家应该生产多少件产品，做几千元的广告，才能获利最大？
某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60） ．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：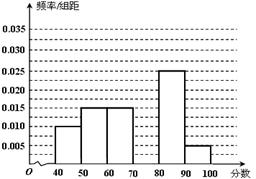
（Ⅰ）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
(Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分；
(Ⅲ) 从成绩是70分以上（包括70分）的学生中选两人，求他们在同一分数段的概率.
（本小题满分12分）
三棱锥
中，
，
,
（1） 求证：面
面
（2） 求二面角
的余弦值．
（本小题满分12分）
已知
，其中向量
, (
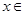R).
（1） 求
的最小正周期和最小值；
（2） 在△ABC中，角A、B、C的对边分别为
、
、
，若
，a=2
，
，求边长
的值.
（本小题15分）已知动圆
被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于
（其中
为圆心，O为坐标原点）。
（1）求a，b所满足的关系式；
（2）点P在直线
上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好在
内”的概率的最大值
（本小题13分）如图1，在三棱锥P—ABC中，
平面ABC，
，D为侧棱PC上一点，它的正（主）视图和侧（左）视图如图2所示。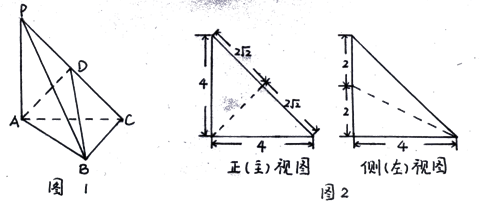
（1）证明：
平面PBC；
（2）求三棱锥D—ABC的体积；
（3）在
的平分线上确定一点Q，使得
平面ABD，并求此时PQ的长。