(本小题15分)已知动圆 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于 (其中
(其中 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。
(1)求a,b所满足的关系式;
(2)点P在直线 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在 内”的概率的最大值
内”的概率的最大值
(本小题10分)
在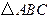 中,
中,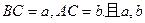 是方程
是方程 的两个根,又
的两个根,又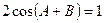 。求:(1)角C的度数;(2)AB的长度。
。求:(1)角C的度数;(2)AB的长度。
(本小题10分)
已知等差数列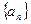 ,
, ,
, ,且项
,且项 分别是某一等比数列
分别是某一等比数列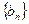 中的第
中的第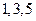 项,(1)求数列
项,(1)求数列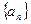 的第12项;(2)求数列
的第12项;(2)求数列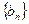 的第
的第 项。
项。
在数列 中,已知
中,已知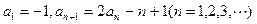 .
.
(1)证明数列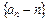 是等比数列;
是等比数列;
(2) 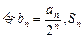 为数列
为数列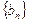 的前
的前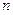 项和,求
项和,求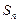 的表达式.
的表达式.
(13分)已知函数 图象上一点P(2,
图象上一点P(2,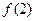 )处的切线方程为
)处的切线方程为 .
.
(1)求 的值;
的值;
(2)若方程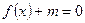 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中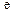 为自然对数的底).
为自然对数的底).
(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率 .直线
.直线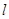 :
: 与椭圆C相交于
与椭圆C相交于 两点, 且
两点, 且 .
.
(1)求椭圆C的方程;
(2)点P(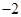 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.