(本小题满分16分)
已知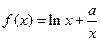 ,求:
,求:
(1)若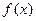 在
在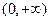 单调递增,求
单调递增,求 范围;
范围;
(2)若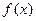 在
在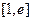 上最小值为
上最小值为 ,求
,求 值;
值;
(3)若存在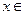
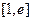 ,使得
,使得 成立,求
成立,求 范围.
范围.
等差数列{ }的前n项和记为Sn.已知
}的前n项和记为Sn.已知
(Ⅰ)求通项 ;
;
(Ⅱ)若Sn=242,求n.
在△ABC中,若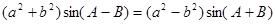 ,请判断三角形的形状
,请判断三角形的形状
已知a=3 ,c=2,B=150°,求边b的长及S△
,c=2,B=150°,求边b的长及S△
某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.