已知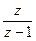 是纯虚数,求
是纯虚数,求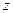 在复平面内对应点的轨迹
在复平面内对应点的轨迹
(本题11分)在△ABC中,角A、B、C的对边分别为 、
、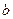 、
、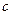 ,且
,且
(1)判断△ABC的形状;
(2)设向量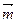 =(2
=(2 ,
,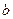 ) ,
) ,  =(
=( ,-3
,-3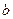 )且
)且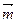 ⊥
⊥ ,(
,(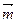 +
+ )(
)( -
-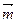 )=14,
)=14,
求S△ABC的值。
(本题10分)已知抛物线C: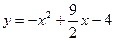 ,过原点O作抛物线C的切线
,过原点O作抛物线C的切线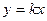 使切点P在第一象限,
使切点P在第一象限,
(1)求k的值;
(2)过点P作切线的垂线,求它与抛物线C的另一个交点Q的坐标。
(本题9分) 已知函数 ,
,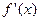 是
是 的导函数
的导函数
(1)求函数 的最小正周期;
的最小正周期;
(2)若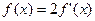 ,求
,求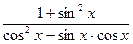 的值。
的值。
函数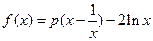 ,
,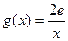 ,
, ,
,
(1)若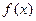 在
在 处取得极值,求
处取得极值,求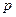 的值;
的值;
(2)若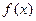 在其定义域内为单调函数,求
在其定义域内为单调函数,求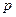 的取值范围;
的取值范围;
(3)若在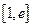 上至少存在一点
上至少存在一点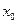 ,使得
,使得 成立,求
成立,求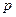 的取值范围.
的取值范围.
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也
需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 的分布列及期望
的分布列及期望 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.