已知函数f（x）= ex－ax－1．
（Ⅰ）若a=1，求证：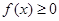
；
（Ⅱ）求函数y=f（x）的值域．
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合，且两个坐标系的单位长度相同．已知直线l的参数方程为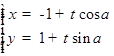
（t为参数），曲线C的极坐标方程为
．
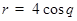（Ⅰ）若直线l的斜率为-1，求直线l与曲线C交点的极坐标；
（Ⅱ）若直线l与曲线C相交弦长为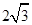
，求直线l的参数方程（标准形式）．
（本小题满分14分）已知函数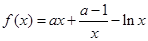
．
（1）若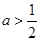
，讨论函数的单调性；
（2）若方程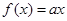
有两个相异实根，求实数
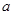的取值范围．
（本小题满分13分）已知椭圆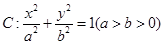
，过焦点垂直于长轴的弦长为1，且焦点与短轴两端点构成等边三角形．
（1）求椭圆的方程；
（2）过点Q（－1，0）的直线l交椭圆于A，B两点，交直线x=－4于点E，若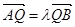
，
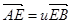，求证λ+μ为定值，并计算出该定值．
（本小题满分12分）已知等差数列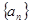
满足：
，
，该数列的前三项分别加上
后顺次成为等比数列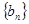
的前三项
（1）分别求数列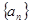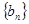，的通项公式
，
；
（2）设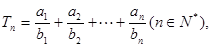
若
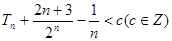恒成立，求
的最小值．
所对的边分别是
，且
。
的值；
，
的面积
，求
的值.