(本小题满分14分)已知椭圆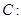
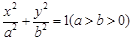 的右焦点为
的右焦点为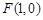 ,且点
,且点 在椭圆
在椭圆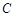 上,
上, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆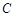 的标准方程;
的标准方程;
(Ⅱ)设过定点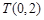 的直线
的直线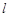 与椭圆
与椭圆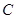 交于不同的两点
交于不同的两点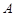 、
、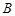 ,且
,且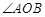 为锐角,求直线
为锐角,求直线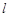 的斜率
的斜率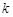 的取值范围;
的取值范围;
(Ⅲ)过椭圆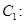
 上异于其顶点的任一点
上异于其顶点的任一点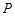 ,作圆
,作圆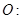
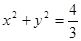 的两条切线,切点分别为
的两条切线,切点分别为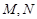 (
(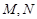 不在坐标轴上),若直线
不在坐标轴上),若直线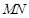 在
在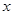 轴、
轴、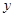 轴上的截距分别为
轴上的截距分别为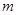 、
、 ,证明:
,证明: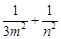 为定值.
为定值.
(本小题满分12分)
如图是函数 的一段图象.
的一段图象.
(I)求 的值及函数
的值及函数 的解析式;
的解析式;
(II)求函数 的最值及零点.
的最值及零点.
(本小题满分12分)
宏达电器厂人力资源部对本厂的一批专业技术人员的年龄状况和接受教育程度(学历)进行了调查,其结果如下表:
| 学历 |
35岁以下 |
35~50岁 |
50岁以上 |
| 本科 |
80 |
30 |
20 |
| 研究生 |
 |
20 |
 |
(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率;
(Ⅱ)在该厂的专业技术人员中,按年龄用分层抽样的方法抽取 个人,其中35岁以下抽
个人,其中35岁以下抽
取48人,50岁以上抽取10人,再从这 个人中随机抽取出1人,此人的年龄为50岁以上
个人中随机抽取出1人,此人的年龄为50岁以上
的概率为 ,求
,求 、
、 的值.
的值.
(本小题满分12分)已知 ,
, ,求
,求 的值.
的值.
(本小题满分12分)
下表是A市住宅楼房屋销售价格 和房屋面积
和房屋面积 的有关数据:
的有关数据: 
(I)画出数据对应的散点图;
(II)设线性回归方程为 ,已计算得
,已计算得 ,
, ,计算
,计算 及
及 ;
;
(III)据(II)的结果,估计面积为 的房屋销售价格.
的房屋销售价格.
本小题满分12分)已知 ,
, ,
, ,且
,且 ,
, ,求点
,求点 及向量
及向量 的坐标.
的坐标.